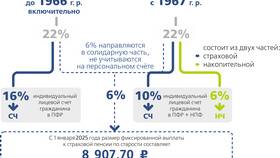
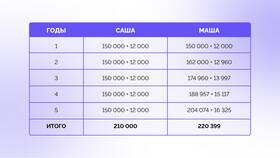
Средний процент - это усредненное значение нескольких процентных величин, которое отражает общую тенденцию или обобщенную характеристику набора данных. Расчет среднего процента применяется в анализе финансовых показателей, успеваемости, статистических данных и других областях.
Содержание
Понятие среднего процента
Основные методы расчета
Среднее арифметическое процентов
Используется, когда нужно найти простое среднее значение нескольких процентных величин:
| Формула | (П1 + П2 + ... + Пn) / n |
| Пример | (10% + 15% + 20%) / 3 = 15% |
Взвешенное среднее процентов
Применяется, когда проценты имеют разную значимость или относятся к разным объемам:
| Формула | (П1×В1 + П2×В2 + ... + Пn×Вn) / (В1 + В2 + ... + Вn) |
| Пример | (10%×100 + 20%×200) / (100+200) = (1000+4000)/300 ≈ 16,67% |
Практические примеры расчетов
Пример 1: Средний процент выполнения плана
- Отдел A выполнил план на 80% (объем 50 ед.)
- Отдел B выполнил план на 90% (объем 30 ед.)
- Отдел C выполнил план на 70% (объем 20 ед.)
- Расчет: (80×50 + 90×30 + 70×20) / (50+30+20) = 81%
Пример 2: Средняя процентная ставка по кредитам
| Кредит | Сумма | Ставка |
| 1 | 100 000 руб. | 12% |
| 2 | 200 000 руб. | 15% |
| 3 | 150 000 руб. | 10% |
| Средневзвешенная ставка | (12%×100 + 15%×200 + 10%×150)/450 ≈ 13,33% | |
Особые случаи расчета
Средний процент изменения
При расчете среднего процентного изменения за несколько периодов используется среднее геометрическое:
- Формула: [(1+П1)×(1+П2)×...×(1+Пn)]^(1/n) - 1
- Пример: рост на 10%, затем на 20%: [(1,1)×(1,2)]^0,5-1 ≈ 14,89%
Средний процент при работе с отрицательными значениями
Когда некоторые проценты отрицательные, обычное среднее арифметическое может дать искаженный результат. В таких случаях рекомендуется использовать медиану или другие устойчивые методы.
Расчет в Excel
| Метод | Функция Excel |
| Среднее арифметическое | =СРЗНАЧ(диапазон_процентов) |
| Взвешенное среднее | =СУММПРОИЗВ(проценты;веса)/СУММ(веса) |
| Среднее геометрическое | =СРГЕОМ(1+диапазон_процентов)-1 |
Пример формулы в Excel:
- Для значений в ячейках A1:A5: =СРЗНАЧ(A1:A5)
- Для взвешенного среднего: =СУММПРОИЗВ(A1:A5,B1:B5)/СУММ(B1:B5)
Типичные ошибки
- Использование среднего арифметического вместо взвешенного для разнородных данных
- Неучет базовых объемов при сравнении процентных показателей
- Неправильная интерпретация среднего процента изменений
- Игнорирование отрицательных процентных значений
Рекомендации
При расчете среднего процента всегда учитывайте:
- Характер данных (однородные/разнородные)
- Наличие весовых коэффициентов
- Особенности изменений (простые или сложные проценты)
- Диапазон значений (возможность отрицательных процентов)
Заключение
Правильный расчет среднего процента требует понимания природы данных и выбора соответствующего метода. Взвешенное среднее чаще всего дает более точные результаты при работе с финансовыми и статистическими показателями, в то время как среднее арифметическое подходит для однородных наборов данных.